日影測定線を掘り下げる
今回は「JG_日影測定線」に関連して、日影図の測定線について掘り下げてみたいと思います。測定線は、閉鎖方式であっても敷地形状や道路線形が複雑になると、基準法の解釈で結果が異なる場合があります。
一般的に測定線は、敷地境界線に対して外側に5mまたは10m離れた点を結んだ線とされます。境界線が凸角になったり凹角になると迷いがちですが、境界線に沿って5mまたは10mの円を転がしたときの軌跡をイメージすると分かりやすくなります。
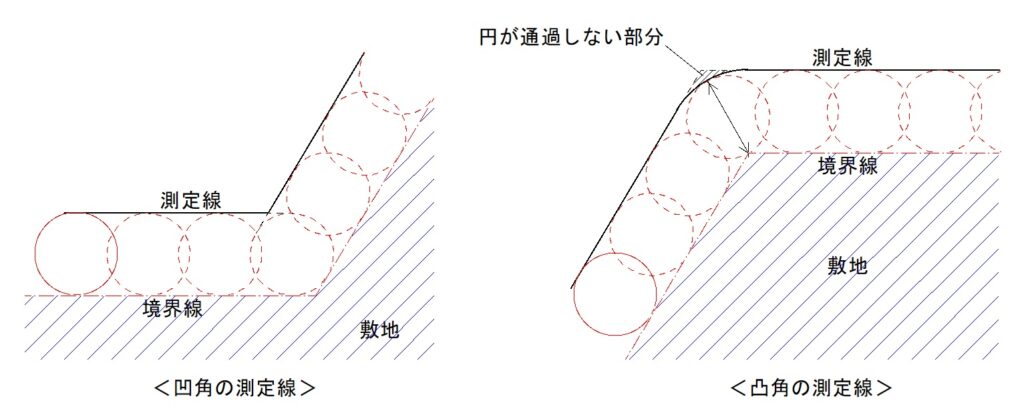
この考え方を基本にすると、測定線は常に連続した閉じた領域をつくります。
少し特殊な例をみて下さい。
次の図は、敷地境界線の折れ点がジグザク状に連続する場合の5mと10mの測定線です。このように入隅と出隅が交互に現れると大小の円弧が連続することになります。

次の図は凹地部分の測定線を示しています。この図のように円弧がクロスする場合、クロスした点から内側にある軌跡は消去されます。

円弧と直線がクロスする場合も同様に内側にある軌跡は消去されます。

さて、道路側の緩和を用いた測定線は、道路形状が複雑になると、法令の解釈の仕方で位置や形状が異なる場合があります。いくつか特徴的なものをみていきたいと思います。
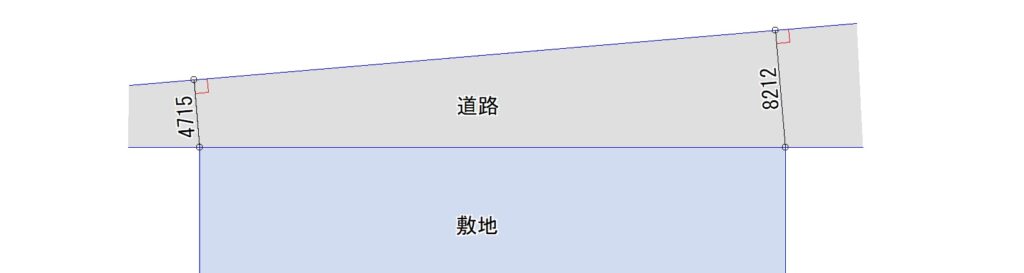
まず道路幅員の取り方ですが、測定線を考える場合、敷地境界線や道路中心線に対して垂線を引くよりも、道路の反対側の境界線に対して垂線を引いて測るのが合理的です。その理由をご説明します。
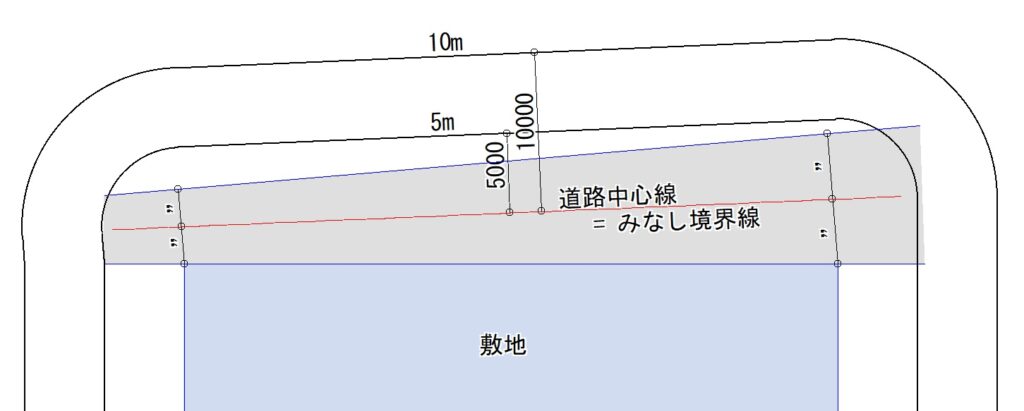
道路の反対側の境界線が敷地境界線と平行ではない場合は、まず道路中心線をA図のように定めます。道路幅員が10m未満の場合は、この中心線が「みなし境界線」となるのは周知のとおりです(A図)。
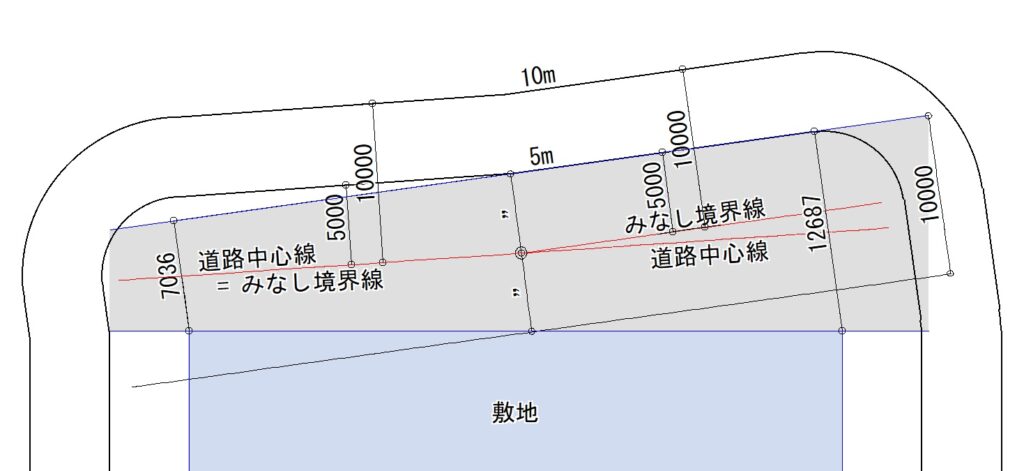
次に、道路幅員が徐々に広がっていき幅員が10m以上になると、反対側の道路境界線が5m測定線になり、そこから敷地側に5m入ったラインが「みなし境界線」になります。みなし境界線は、幅員が10mまでは中心線に重なり、10m以上で敷地の反対側に枝分かれしていきます。
B図の◎の位置に着目して下さい。幅員が10mの位置で反対側の境界線から垂直に敷地境界線に下した線の中点と、みなし境界線が枝分かれする点が一致しています。これは、道路幅員を反対側の境界線に対して垂直にとっているためです。道路中心線(二等分線)に対して垂線をとるとこの点は一致しません。
余談ですが本ツールにおいて、八の字状の道路のみなし境界線を厳密な道路中心線(角度の二等分線)にするか上記のようにするかは試行錯誤がありました。実際の道路はミクロ的にみると単純な直線で構成されることはなく、中心線というのは結局のところ「安全側に設定した仮想ライン」の域を出ないのではないかと考えます。つまり、道路幅員の中点を道路中止線が通ってさえいればよいのではないかと考察しています。
さて次に「みなし境界線」の位置を特定しづらいクランク状の道路について考えたいと思います。
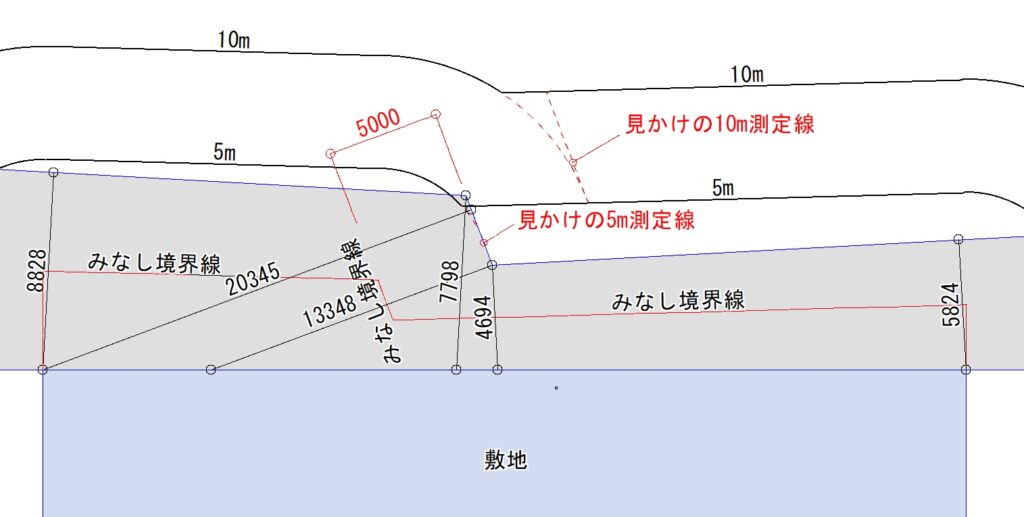
G図は、反対側の境界線の一部が敷地に直角に近い状態にまで折れていて、そのため幅員が10mを超えるような場合です。この場合みなし境界線の位置は、道路中心ではなく反対側から5mの位置になります。理由は幅員が10m以上になるためです(B図参照)。しかし5m測定線は出隅処理の過程で無くなり(ロ図参照)、あくまで見かけの測定線になってしまいます。10m測定線も同様です。
出隅を円弧にしない場合もありますが、「JG_日影測定線」では出隅部を必ず円弧で処理します。
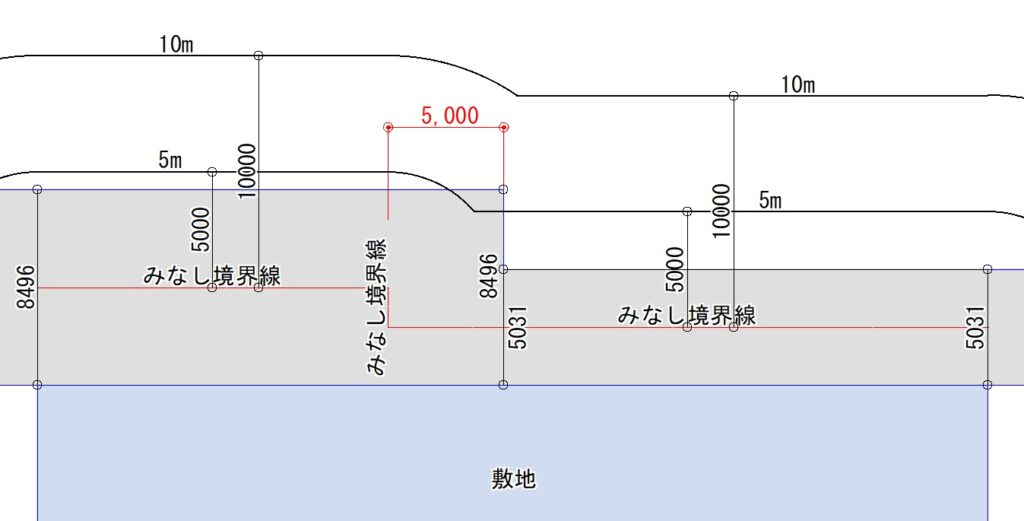
H図は、G図の反対側の境界線が完全に垂直になった(「かぎ型」になった)場合です。この場合も同様の考え方を用いて、反対側から5mの位置をみなし境界線としています。
一方でこの雁行道路には、次の解法も存在します。

この図は一般的に「幅員の異なる道路が雁行する場合のみなし境界線の位置」として行政の手引書などに登場します。
この解法では、幅員が切り替わる位置が「みなし境界線」になっています。出隅部も円弧として処理されていません。ただこの考え方は、G図のように傾きがある場合にはその解決策を与えてくれません。
さて、対岸が敷地の場合はどうでしょうか。
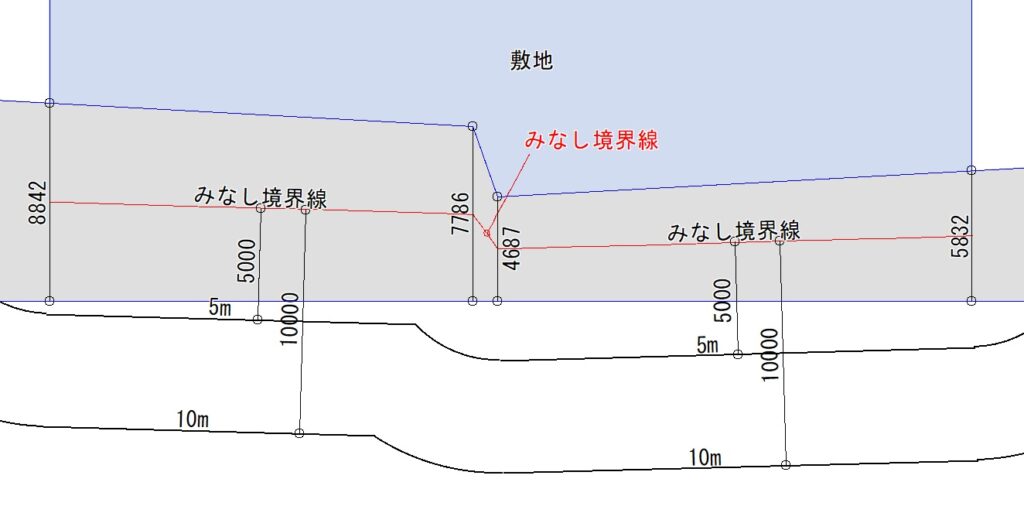
J 図は、G図と同じやや崩れた「かぎ型」の境界線です。本ツールでは、この場合も反対側の道路境界線に垂直に引いた幅員線の中点をつないで「みなし境界線」とします。
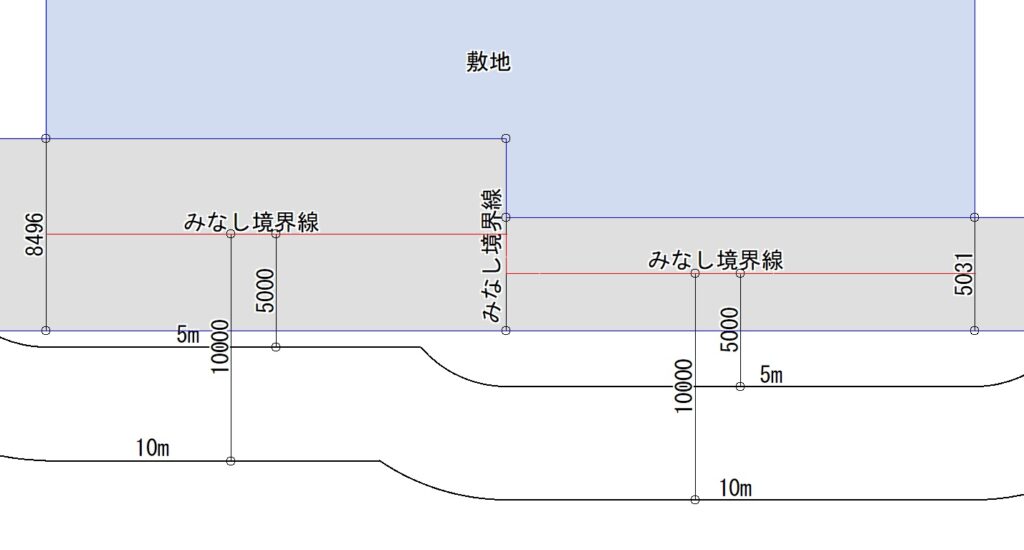
J図が完全な「かぎ型」になったK図においても、J図の中央部分が閉じるかたちで「みなし境界線」が設定されます。奇しくもI図と同じになりました。ただし測定線は一貫して円弧になります。
ここまでみてくると、「JG_日影測定線」のプログラムを用いた解法にはある程度一貫性があります。これらの解法がすべての特定行政庁で受け入れられるかというと、そうではないかもしれませんが、アルゴリズムを用いて「みなし境界線」を一意に定めることは可能と言えるかもしれません。
ただし次の、隣地境界線と道路の「みなし境界線」の結合方法については、実務の状況から二通りの解法を用意せざるを得ません。

L図は、道路の「みなし境界線」の結合について、隣地境界線を道路のみなし境界線まで延長して閉じた領域をつくる手法です(結合方法1とします)。自治体が配布している手引書に多い解法です。

一方でM図は、道路に垂直な「みなし境界線」を介して閉じた領域をつくる手法です(結合方法2とします)。逆日影ソフトなどで採用していることが多い解法です。「JG_日影測定線」(Ver.1.1以降)ではどちらの方法も選択できます。

ところで、道路際が隅切のように道路と接する際に結合方法1を採用するとどうなるでしょうか。N図のように著しく不利な状況が発生します。結合方法1の盲点なのか、本来は発散方式とセットでの運用を意図されていたのか、真相は分かりません。
発散方式の解法については、東京都安全条例の解説にその説明がありますが、道路形状が複雑な場合(道路が雁行していたり屈曲している場合)や交差点になっている場合はほとんど触れられていません。そのせいか様々な解法が用いられていて迷走に近い状況です。いくつか特徴的なものを紹介します。
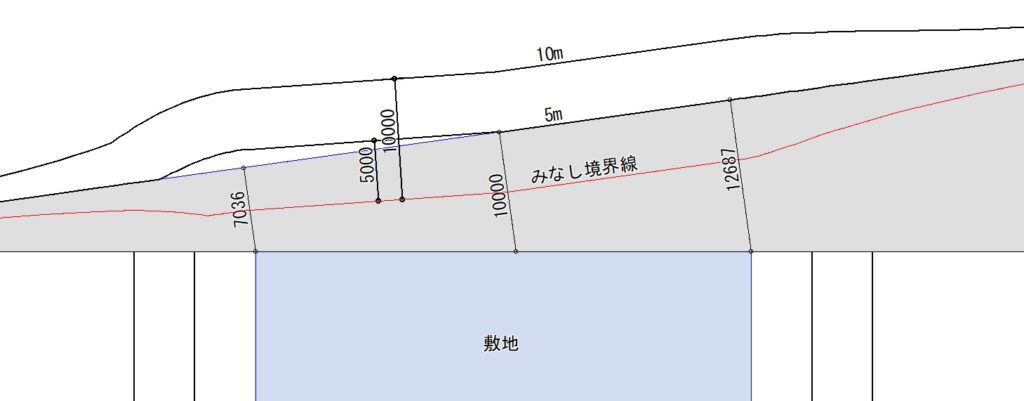
発散方式で測定線を描画すると道路幅員が10m未満であっても道路内に測定線が発生しません。東京都安全条例の解説にもありますが、このことから「発散方式は道路内を一律緩和するもの」と言われています。満更間違いではないと思います。このことを踏まえて次の図をみてください。
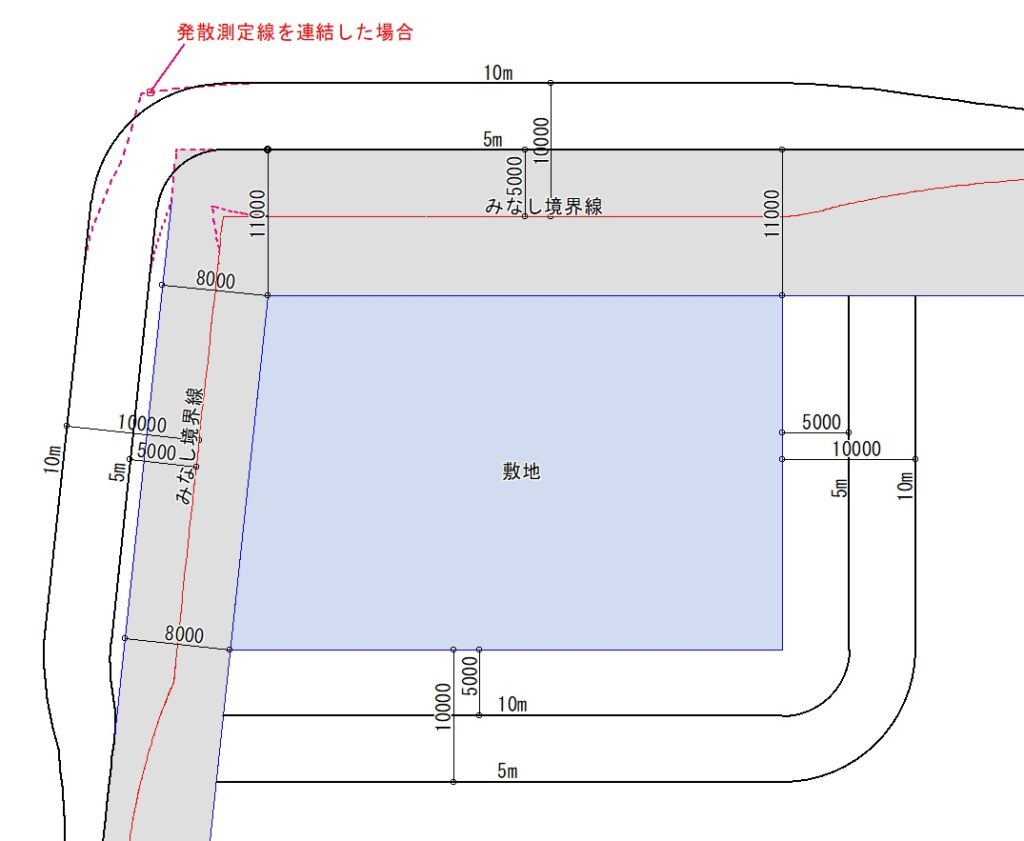
前面道路が屈折する場合の発散方式による解法です。この場合二通りの解法が考えられます。一つは、発散方式で作成した測定線を相互に交わらせる方法、もう一つは、閉鎖方式を採用して円弧にする方法です。P図をみると分かるように、閉鎖方式を採用すると道路に測定線の一部がかかります。発散方式と閉鎖方式を併用するのは良くないというのも頷けます。
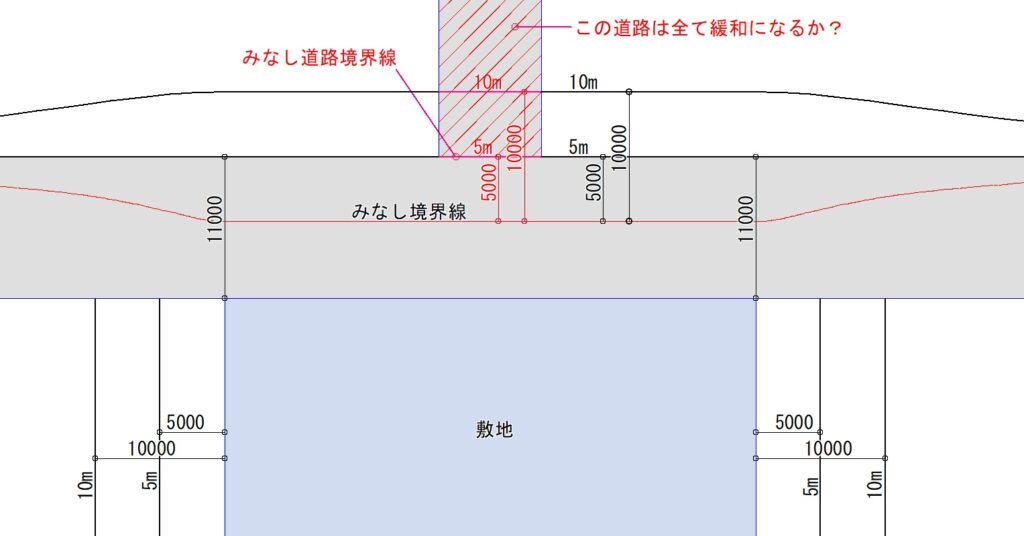
次に、Q図のように前面道路に直交する道路がある場合です。この直交道路に発散方式を採用できるでしょうか。敷地の端部が交差点の場合に採用しているのをみかけますが(個人的には疑問ですが)、Q図にこの考え方を準用するのは困難です。そうかといって道路内を全て緩和するのは行き過ぎな感じがします。道路斜線制限などでは街区を整えるため「みなし道路境界線」を敷地の反対側に設定しますが、この考え方を準用すると、測定線は直交道路で分断されずに連続することになります(Q図)。ひとつの落としどころかもしれません。
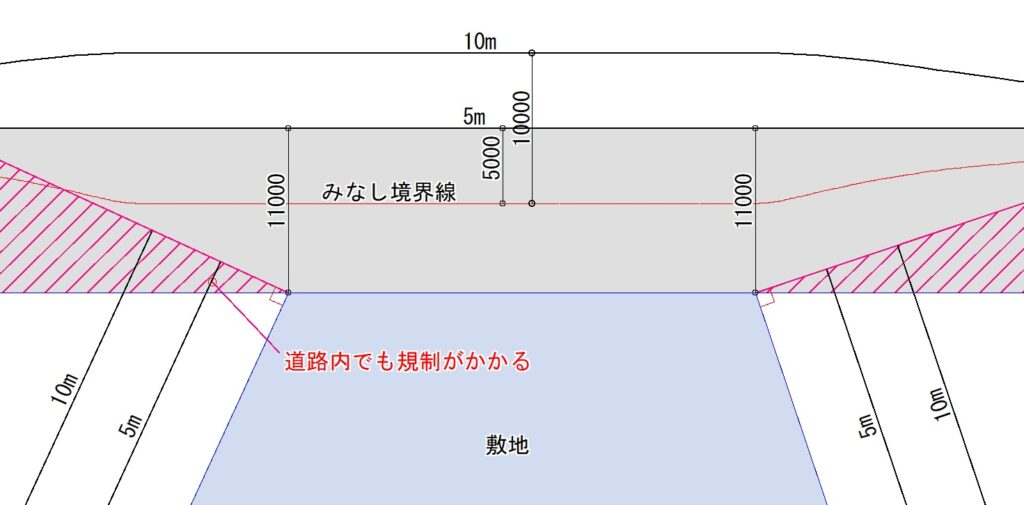
さて、行政庁によっては、先のL図のように敷地境界線が道路に鈍角に取り合う場合、道路内であっても敷地側の測定線が延伸するとみなされます(R図)。これは発散方向の無制限の緩和を抑止する考え方で、閉鎖方式と発散方式の折衷案と捉えてもよいかもしれません。
コメントを残す